전자 광학 센서는 크게 두 파트. 광학계와 검출기로 구성되어 있습니다. 그 중 렌즈라고하는 광학계는 Scene으로부터 나온 빛(전자기파)을 한 지점으로 모아주는 역할을 합니다. 빛을 모으는 이유는 scene으로부터 한 방향으로 나온 빛은 매우 약하기 때문에 빛의 굴절 원리를 이용해서 최대한 많은 양의 빛을 검출기(detector)에 맺히도록 하는 것입니다.
사실 DSLR 카메라와 같은 사진에 관심이 많은 사람들이 렌즈에 대한 이해도가 더 깊을수 있습니다. 다만, 여기서는 어떻게 하면 사진을 잘 찍을까가 아닌 빛을 모아주는 렌즈의 광학적 원리에 대해 얘기하고자 합니다.
렌즈 기본
렌즈라 함은 쉬운 예로 안경을 생각하면 됩니다. 빛이 망막에 모이도록 굴절시키는 눈의 능력이 떨어져 안경의 렌즈가 한 점에 모이도록 눈의 역할을 대신하는 것이죠. 렌즈도 외부로부터 카메라로 들어오는 빛을 한점으로 모으는 역할을 합니다.
렌즈는 형상에 따라 볼록(convex)렌즈와 오목(concave)렌즈로 구분할 수 있는데, 렌즈를 통과한 후 ray(빛)의 진행방향은 각각 다릅니다.
렌즈를 기하광학 관점으로 이해하기 위해서는 앞에서 설명했던 빛의 굴절을 이해해야 합니다.
(*이전 포스팅을 참고하세요)
렌즈의 원리를 공부하는데 있어 가장 먼저 광선추적법(ray-tracing)이라고 부르는 세 가지 원리를 이해해야 합니다. 광선 추적법은 다음과 같습니다.
(1) 렌즈 주축(principal axis)에 평행하게 입사한 ray는 렌즈를 통과하며 반대편 초점을 통과한다.
(2) 렌즈 초점을 지나며 입사한 ray는 렌즈를 통과 후 평행하게 진행한다.
(3) 렌즈의 중심을 통과한 ray는 굴절없이 그대로 일직선으로 진행한다.
아래 그림으로 자세히 알아보겠습니다. (이때 렌즈의 두께는 매우 얇다고 가정합니다. 실제 두께가 있는 렌즈에서는 렌즈로 ray가 들어올때와 나갈때 두번 굴절되기 때문에 복잡해 집니다.)
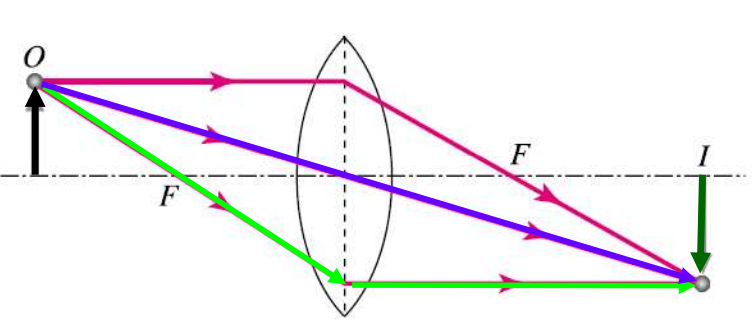
위 그림에서 F는 초점(렌즈 중심을 기준으로 양쪽 같은 거리에 있습니다.)을 의미하고 빨간색 ray가 (1), 녹색 ray가 (2), 보라색 ray가 (3)번 원리에 따른 광선의 움직임을 보여주고 있습니다.
ray가 렌즈를 통과하며 이 원리를 따르는 것은 공기와 렌즈의 굴절률 차이에 따라 빛의 진행방향이 굴절되기 때문입니다. (Snell의 법칙 - 앞장에서 살펴보았습니다. )
초점의 위치는 아래와 같이 매질의 굴절률(n)과 렌즈의 곡률 반경(R)에 의해 결정됩니다. 즉, 빛이 렌즈를 통과하며 얼마나 많이 굴절되는지, 혹은 렌즈가 얼마나 둥글게 혹은 납작한 형상을 가지고 있는지에 따라 초점이 결정되죠.

볼록렌즈(convex lens)
물체에서 나온 빛이 렌즈를 통과한 후, 상이 맺히는 원리를 살펴보겠습니다.
첫번째 케이스로 물체가 초점거리의 2배보다 더 멀리 있는 경우입니다.

위 그림에서 실제 물체(녹색 화살표)에서 반사되어 렌즈의 축과 평행하게 진행하는 ray는 렌즈를 통과한 후 반대쪽 초점(f)을지나도록 굴절됩니다. 화살표 끝에서 반사되어 같은쪽 초점을 지나도록 진행하는 ray는 렌즈를 통과하며 축과 평행하게 진행하도록 굴절되어 한점에서 만납니다.
이렇게 화살표의 모든 점에서 반사된 ray는 렌즈 반대편 한 지점에 상이 맺히게 됩니다. (빨간색 화살표) 이는 실제로 맺힌 상이고(real) 뒤집혀 상이 맺히게 되며(inverted) 크기는 실제보다 작게 됩니다.(demagnified)
두번째 경우로 물체가 정확하게 초점거리의 2배 거리에 있는 경우입니다.

예상은 했겠지만 렌즈를 중심으로 양쪽의 기하가 symmetric 이므로 렌즈 반대쪽에 맺히는 상은 실제 물체와 크기가 정확하게 같습니다.
세번째 경우는 물체가 초점거리과 초점거리의 2배 사이에 있는 경우입니다.

이 경우 맺히는 상의 크기는 실제 물체보다 커지게 됩니다. (magnified)
네번째 경우는 물체가 초점과 같은 위치에 있는 경우입니다. (노란색 화살표)
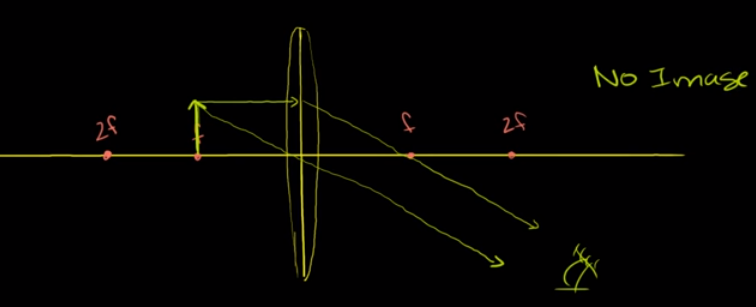
물체가 초점 상에 있는 경우는 좀 특이합니다. 평행하게 진행하는 ray는 반대쪽 초점을 지나게 되고 렌즈의 중심을 통과하는 ray는 그대로 진행합니다. 그림을 보면 알겠지만 이 두 ray는 평행하게 진행하여 한 점에서 만나지 않습니다. 따라서 렌즈의 반대쪽에는 상이 맺히지 않게 됩니다. 즉 반대쪽에서는 물체의 상을 볼 수 없게 되죠.
마지막 경우로 물체가 초점보다 렌즈와 더 가까운 위치에 있는 경우입니다.

이 경우 축과 평행하게 진행하는 ray와 초점을 지나도록 진행하는 ray는 렌즈의 반대편이 아닌 물체와 같은 쪽에 상이 맺힌 것처럼 보입니다. 하지만 실제로 ray가 모여서 생긴 상이 아니고(virtual), 맺힌 상은 물체와 방향이 같고 (up-right) 맺힌 상의 크기는 실제 물체보다 더 큽니다. (magnified). 대부분의 확대경은 이 원리를 이용한 것입니다.
추억을 소환해보면 학창시절 현미경으로 관찰할때 둥근 조절 나사를 이용해 렌즈의 위치나 관찰할 물체 받침대를 위, 아래로 움직였던 기억이 있습니다. 그때부터 우리는 초점을 맞추거나 물체를 확대해서 보기 위해 렌즈를 사용하고 있었던 것입니다.
오목렌즈(concave lens)
오목렌즈는 볼록렌즈에 비해 단순합니다. 오목렌즈를 통과한 ray는 볼록렌즈와는 달리 발산하는 방향으로 굴절됩니다.

위 그림과 같이 렌즈 반대쪽에서 물체를 바라봤을때 물체에서 나온 ray는 관찰자의 눈에 맺히는 것이 아니라 물체와 같은 쪽에 상이 맺히는 것처럼 보이게 됩니다. 이러한 원리로 오목렌즈일 경우 물체의 위치에 관계없이 항상 축소된 정립허상으로 보이게 됩니다.
초점거리와의 관계 (Thin lens equation)
그렇다면 실제 물체의 위치와 초점거리에 따라 상은 어디에 맺히게 될까요? 이는 아래와 같은 간단한 수식으로 관계를 정리할 수 있습니다.
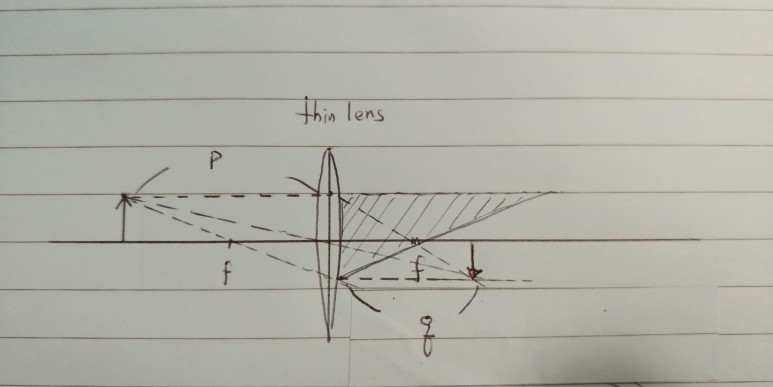
위 그림은 일반적인 thin 볼록렌즈에서 상이 맺히는 원리를 나타냅니다.
초점거리가 f인 렌즈에서 물체까지의 거리를 p, 상이 맺히는 곳까지의 거리를 q라고 하겠습니다. 물체에서 나온 두 ray가 렌즈 왼쪽에서 만드는 삼각형을 렌즈를 기준으로 대칭이동 했을때 빗금친 삼각형을 만들어 낼 수 있습니다.
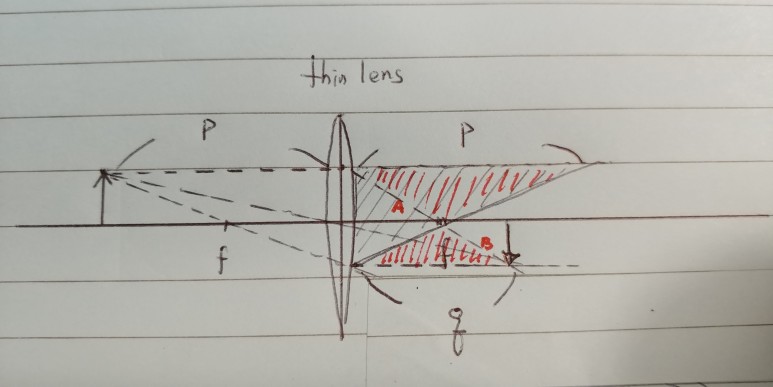
이때 빨간색으로 빗금친 두 삼각형은 닮음이 되고 대변인 p와 q의 길이의 비는 A와 B의 비와 같습니다.

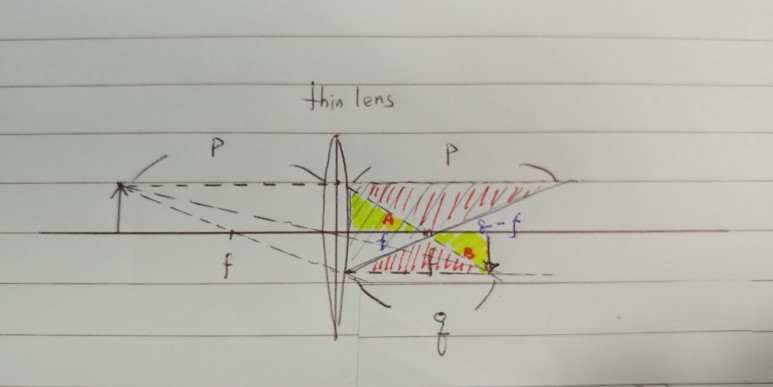
다시 노란색 두 직각삼각형은 닮음이 되고 역시 대응하는 A와 B의 길이의 비는 f와 q-f의 비와 같습니다.

따라서 위에서 정의한 p와 q의 길이의 비는 f와 (q-f)의 비와 같게 됩니다. 이를 정리하면 아래와 같은 thin lens equation을 유도할 수 있습니다.

위 thin lens equation에 따라 매우 멀리있는 물체는 어디서 보아야 초점이 맞는 상을 볼 수 있을지 예측해 보겠습니다.
(다시 한번 변수의 의미를 복기하면, p는 렌즈에서 물체까지의 거리, q는 렌즈에서 상이 맺히는 위치까지의 거리, f는 렌즈의 초점 거리입니다.)
p가 매우 커지면 1/p은 0으로 수렴하고 그러면 q는 f에 수렴합니다. 즉, 아주 먼 곳에 있는 물체는 초점거리에 해당하는 f에서 바라봐야 초점이 잘 맞는 상을 획득할 수 있습니다. 이 의미를 거꾸로 생각해보면 상이 맺히는 디텍터를 초점에 설치하면 멀리 있는 scene은 뚜렷한 상을 얻을 수 있다는 의미이지요.
이러한 원리는 전자광학 시스템의 광학계 및 검출기 설계에 매우 중요하게 반영됩니다.
우리가 흔히 볼 수 있는 현미경이나 망원경은 여러개의 렌즈조합으로 만들어집니다. 물론 렌즈 설계는 어렵지만 렌즈의 기본적인 광학적 원리만 이해해도 영상센서를 공부하는데는 무리가 없습니다.
오늘은 이만 줄이겠습니다. 감사합니다.
[함께 읽어보면 좋은 포스팅]
전자광학 공부를 위한 광학 기초 - 1. 반사와 굴절
전자광학(EO/IR) 영상 센서를 이해하기 위해서는 기하광학 이라는 분야에 대한 이해가 필요합니다. 광학이라고 해서 어려울건 없습니다. 저도 비전공자인만큼 최소한의 것만 알고 넘어갈것이니
mkpark.tistory.com
[출처] 직접작성 (last updated: 2021.02.27)
[참고자료]
Khanacademy: Geometric optics
https://www.khanacademy.org/science/physics/geometric-optics/modal/v/refraction-in-water
http://phya.snu.ac.kr/php/subject_list/Notice/data/1417963785.pdf
블로그의 모든 포스팅은 직접 공부해서 작성한 글입니다.
퍼가실 때는 댓글을 남겨주세요.
더 유익한 포스팅을 작성하는데 큰 힘이 됩니다.
'전자광학' 카테고리의 다른 글
| 전자광학 시스템의 광학계 (Optical system) (0) | 2021.03.09 |
|---|---|
| 전자광학 공부를 위한 광학 기초 - 3. 편광 (0) | 2021.03.05 |
| 전자광학 공부를 위한 광학 기초 - 1. 반사와 굴절 (0) | 2021.02.23 |
| 온도를 가진 것은 에너지를 내뿜는다 - 흑체 복사 (Black body radiation) (2) | 2021.02.03 |
| 전자광학(EO)/적외선 (IR) 스터디 (2) | 2021.02.01 |